Cryptocurrency portfolio optimization using Markowitz theory in Holderlab.io. The great Harry Markowitz in 1952 wrote the work “Portfolio Selection” for which he received the Nobel Prize only in 1990. It is based on the theory of the distribution of assets between various financial instruments.
According to Markowitz, any investor should base his choice solely on expected returns and standard deviation when choosing a portfolio. Thus, having carried out an assessment of various combinations of portfolios.
Must choose the “best” one, based on the ratio of the expected return and the standard deviation of these portfolios. The ratio of the return-risk portfolio remains normal: the higher the yield, the higher the risk.
Modern Portfolio Theory
In Cryptocurrency portfolio optimization using Markowitz theory. Markowitz put two parameters at the head of his theory – risk and profitability. An efficient frontier is one that defines the effective set of portfolios on it, respectively, between risk and return. Let’s look at an example:
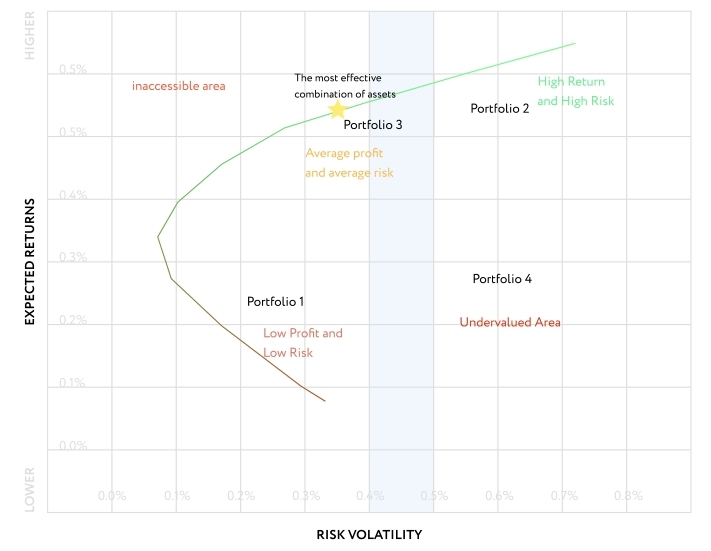
Low return and low risk – Portfolio 1
High return and high risk – Portfolio 2
Effective portfolio – Portfolio 3
Not effective portfolio – Portfolio 4
All investment portfolios that are on the border will be effective. With the existing risk, the other portfolio will have lower returns. Therefore, the investor can choose the appropriate risk and select the optimal yield.
Cryptocurrency portfolio optimization with Holderlab.io
Before start you can check correlation matrix of your portfolio. The service allows you to evaluate the analysis of options – 5,000 portfolios. The results are the conclusion of three portfolios and determination of their weights, such as the optimal portfolio, the minimum volatility and the most volatile portfolio, depending on the Sharpe ratio.
To start cryptocurrency portfolio optimization:
- Go to the efficient frontier tool
2.Select the cryptocurrencies you are interested in using search or scroll and add it.
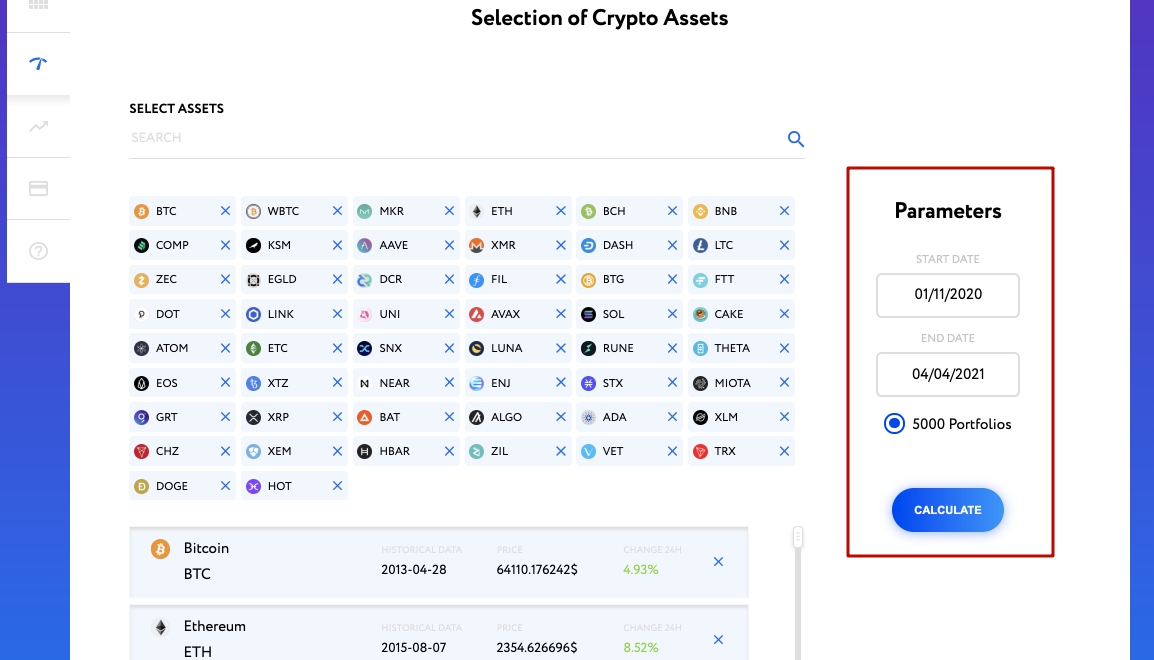
Choosing parameters for optimizing a cryptocurrency portfolio
3. Indicate in the parameters the date for the beginning of the analysis and the end date of the historical period, for example, the last 6 months, select the parameter 5000 portfolios. For more information about subscription options, see the Subscriptions section. After that, click the “calculate” button
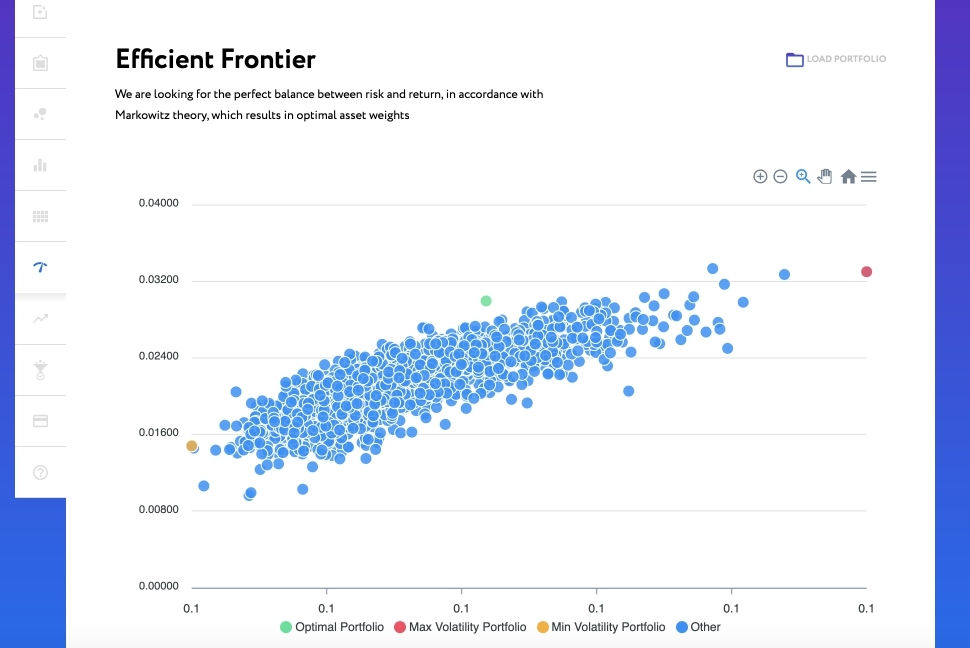
Efficient frontier distribution graph
4. After processing, you will see a graph of the distribution of borders. The green circle is the minimum volatile portfolio according to the Markowitz method, the yellow circle is the minimum volatile portfolio according to the Markowitz method. The blue circle is the rest of the analyzed portfolios that do not meet the boundary search requirements.
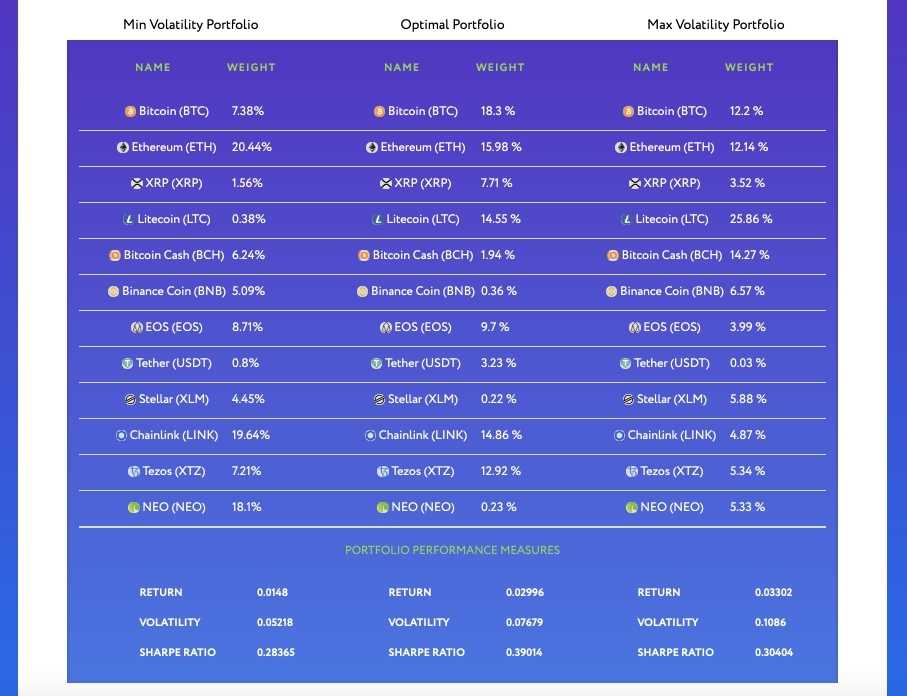
5. Below you will see the details of the analyzed portfolio and the determination of the cryptocurrency weights in the portfolio obtained using the efficient frontier. In addition, you will see a portfolio assessment by Sharpe ratio, volatility and return.
The optimal cryptocurrency portfolio
The optimal portfolio is calculated by the maximum value of the Sharpe ratio. The analysis below is not a template for investing, but shows the results of the operating mode of the “effective border” tool for the purpose of familiarization.
Saving the results of optimization of the cryptocurrency portfolio
Then you can save the results of your portfolio and switch to the backtest mode. In order to save the portfolio, select the portfolio you are interested in, give it a name and click the “save” button.
Thank you for read guide about cryptocurrency portfolio optimization using Markowitz theory. To learn more about portfolio testing, check out the backtest topic.
